МатОлимп #8
Сегодня у нас простенькая задача, балла на 4 из 10. Условия выглядят следующим образом
Делаем небольшую паузу, пьём кофе, смотрим мем и начинаем решать.
Теперь можно и приступить к разбору.
Давайте разберёмся, какие остатки от деления на три может давать квадрат числа. Произвольное число даёт в остатке от деления на 3 либо 0, либо 1, либо 2. Такие числа соответственно можно записать в виде 3k, 3k+1 и 3k+2. Рассмотрим их квадраты.
Первый квадрат имеет остаток 0, а два оставшихся имеют остаток 1.
Отсюда следует, что x и y не могут одновременно давать остаток и 1 и 2 от деления на 3 ( иначе z имело бы в остатке 2, а это запрещено для квадрата, как мы увидели выше ). Следовательно, одно из этих чисел делится на 3.
Теперь поглядим на остатки от деления на 8. Произвольное число при делении на 8 даёт в остатке либо 0, либо 1, либо 2, либо 3 и тд до 8. Эти числа записываются как 8k, 8k+1, 8k+2, 8k+3 и тд до 8k+7.
Посмотрим на остатки их квадратов.
Так как z^2 не может давать в остатке что-то отличное от этих чисел, то приходим к выводу, что либо левая часть даёт в сумме остаток 1 ( а это значит, что одно из чисел делится на 8), либо оба числа дают в остатке по 4. В первом случае все очевидно, так как какое-то число делится на 3 да еще одно из них на 8. Значит произведение делится на 24 (а на 12 и подавно). Во втором случае, если глянем на табличку, заметим, что оба числа будут делится на 2. Значит их произведение делится на 3 и на 4 ( по 2 от каждого числа). Таким образом xy делится на 12. Задача решена!




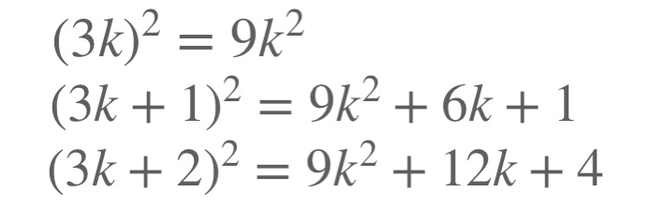
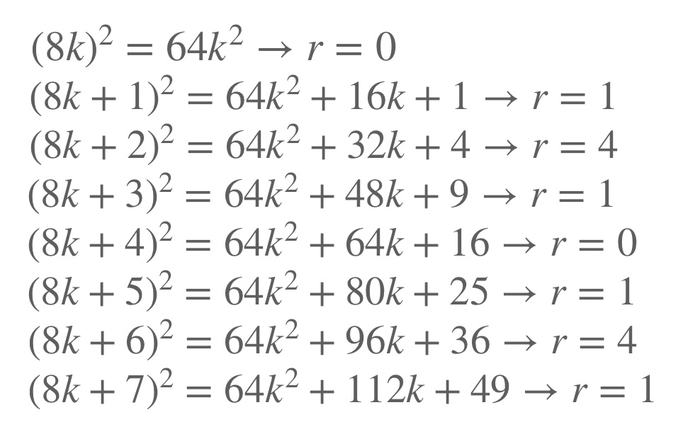

Лига математиков
622 поста2.4K подписчика